素彩office教程

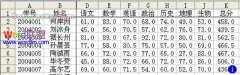
　　某班级期中考试进行后，需要统计成绩的平均值、区间，以及给出班级内部学生成绩差异的量化标准，借此来作为解决班与班之间学生成绩的参差不齐的依据。要求得到标准差等统计数值。

　　样本数据分布区间、标准差等都是描述样本数据范围及波动大小的统计量，统计标准差需要得到样本均值，计算较为繁琐。这些都是描述样本数据的常用变量，使用Excel数据分析中的“描述统计”即可一次完成。

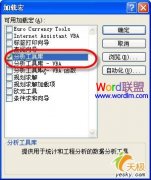
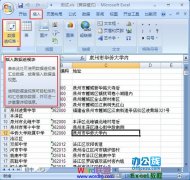
　　本功能需要使用Excel扩展功能，如果您的Excel尚未安装数据分析，请依次选择“工具”-“加载宏”，在安装光盘中加载“分析数据库”。加载成功后，可以在“工具”下拉菜单中看到“数据分析”选项。

　　①打开原始数据表格，制作本实例的原始数据无特殊要求，只要满足行或列中为同一属性数值即可。



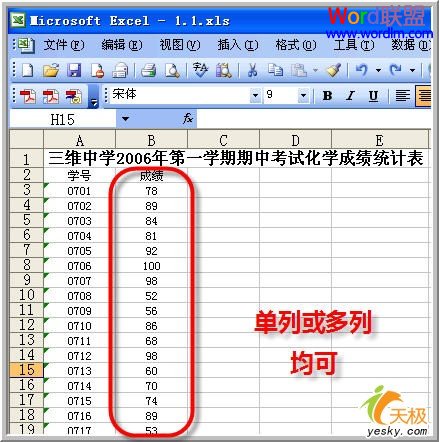
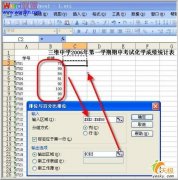
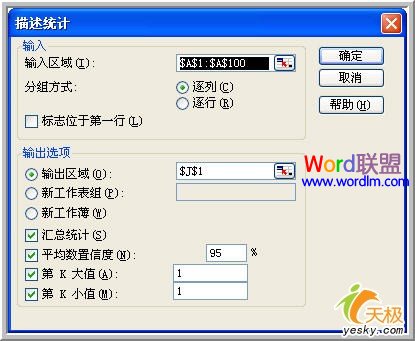
　　②选择“工具”-“数据分析”-“描述统计”后，出现属性设置框，依次选择：

　　输入区域：原始数据区域，可以选中多个行或列，注意选择相应的分组方式；

　　如果数据有标志，注意勾选“标志位于第一行”；如果输入区域没有标志项，该复选框将被清除，Excel将在输出表中生成适宜的数据标志；

　　输出区域可以选择本表、新工作表或是新工作簿；

　　汇总统计：包括有平均值、标准误差(相对于平均值)、中值、众数、标准偏差、方差、峰值、偏斜度、极差、最小值、最大值、总和、总个数、最大值、最小值和置信度等相关项目。

　　其中：

　　中值：排序后位于中间的数据的值；

　　众数：出现次数最多的值；

　　峰值：衡量数据分布起伏变化的指标，以正态分布为基准，比其平缓时值为正，反之则为负；

　　偏斜度：衡量数据峰值偏移的指数，根据峰值在均值左侧或者右侧分别为正值或负值；

　　极差：最大值与最小值的差。

　　第K大(小)值：输出表的某一行中包含每个数据区域中的第 k 个最大(小)值。

　　平均数置信度：数值 95% 可用来计算在显著性水平为 5% 时的平均值置信度。



　　结果示例如下(本实例演示了双列数据的描述统计结果)：